Dans la vie faut se faire plaisir
Comment obtenir de l’audience sur un sujet qui n’intéresse que moi-même et une poignée de personnes ?
La réponse est (à peine) masquée dans le présent article…
Go Home est un petit jeu Flash bien sympa, dans lequel vous devez échanger 2 bonshommes de maison sans qu’aucun des 2 ne prenne le même chemin que l’autre.
Bon ok c’est pas très clair dit comme ça donc je vous invite à cliquer sur How to Play ci-dessous, ou …
… à lire la suite de cet article !
Les 7 ponts de Königsberg
Les plus matheux d’entre vous auront reconnu une problématique très proche du fameux problème des 7 ponts de Königsberg, inspiration première de la Théorie des graphes, et de la Topologie en maths (ça me rappelle de très mauvais souvenirs finalement…)
Je ne rentrerai pas dans le vif du sujet pour 2 raisons :
- Ca va faire fuire les 3 lecteurs de ce blog que j’ai eu tant de mal à capter
- Je suis assez mauvais en maths (un bon 0,5 à une des épreuve du concours de l’ENS le confirme…)
Mais je vais me faire plaisir (comme indiqué ci-avant) et quand même vous présenter rapidement le problème des 7 ponts de Königsberg (m’en fous c’est mon blog et je fais ce que je veux ! Et toc ! )
Alors c’est quoi ce fameux problème ?
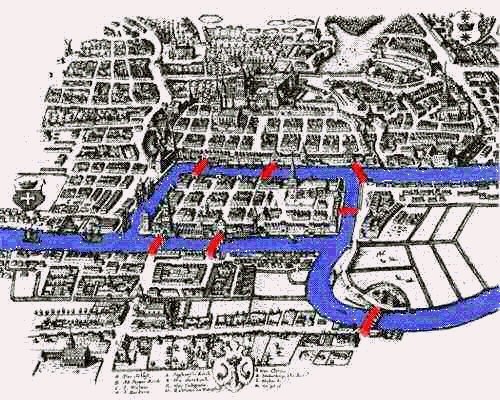
La ville de Königsberg (aujourd’hui Kaliningrad) est construite autour de deux îles reliées entre elles par un pont et six ponts relient le continent à l’une ou l’autre des deux îles.
Le problème consiste à déterminer s’il existe ou non une promenade dans les rues de Königsberg permettant, à partir d’un point de départ au choix, de passer une et une seule fois par chaque pont, et de revenir à son point de départ, étant entendu qu’on ne peut traverser le Pregel qu’en passant sur les ponts.
Les 7 ponts
Schématisation du problème
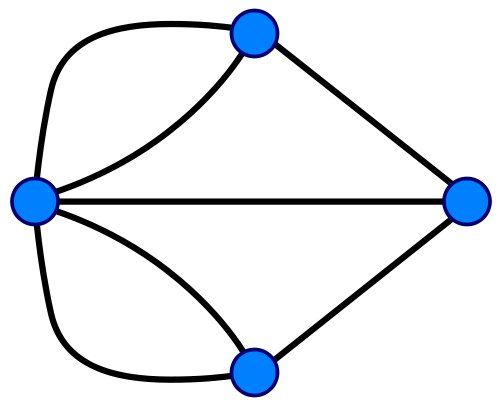
Représentation topologique du problème
La distance entre les ponts, ou leur longueur n’ont aucun impact sur la ou les solutions au problème.
La dernière représentation est donc une vue « générique » du problème.
Euler a démontré … qu’il n’existe AUCUNE promenade qui réponde aux hypothèses, donc pas la peine de vous casser la tête à essayer d’en trouver une.
Par contre j’espère que le concepteur du Jeu en Flash a pris le soin de vérifier la même chose pour ses tableaux sinon vous risquez fort d’être bloqué 🙁
Donc maintenant vous allez pouvoir frimer et raconter à vos amis que pour vous détendre vous résolvez des problèmes de Math avancés.
Je vous ai saoulé ? Bon … vous pouvez aussi me dire « Go home » 😉
-
Need For Speed Hot Pursuit Remastered (Nintendo Switch)Foncez sur les routes sinueuses de Seacrest Country dans des courses socialement compétitives Obtenez tous les principaux contenus téléchargeables publiés au lancement plus 6 heures de jeu supplémentaires et plus de 30 défis Pilotez les supercars les plus convoitées au monde des deux côtés de la loi Affrontez vos amis ou jouez en solo en mode carrière pour remporter des Primes et débloquer de s voitures armes et équipements L’expérience de course intemporelle Need for Speed Hot Pursuit Remastered a été remise à niveau pour les systèmes actuels avec des graphismes améliorés
-
Mario + The Lapins Crétins: Kingdom BattleEmbarquez avec votre équipe de héros dans une quête épique pour libérer vos amis et ramener l’ordre dans le Royaume Champignon ! Explorez quatre mondes iconiques remplis de coffres et de secrets, résolvez des énigmes et soyez plus malins que vos ennemis, imprévisibles sur le champ de bataille. Découvrez un jeu de combat et d’aventure unique et déjanté basé sur un système de combat au tour par tour et profitez d’un arsenal composé de plus de 250 armes. Jouez avec un ami en multijoueur local : partagez une paire de manettes Joy-con avec votre ami ou utilisez les manettes de votre Nintendo Switch Pro. Mettez vos compétences tactiques à l’épreuve avec le Mode Versus et opposez-vous à un ami avec une équipe de 3 héros, à travers des champs de bataille uniques remplis de bonus. Vous pouvez aussi relever des défis à deux avec le Mode coopération, défis jouables avec trois niveaux de difficulté.
